Author:
(1) David Staines.
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
F Abstract Algebra
This section supplies an introductory primer on homological algebra, De Rham cohomology and category theory, complimentary to the informal discussion in the text. Each occupies a subsection. At the end, a short part is devoted to additional details of a calculation from Proposition 20, which applies the methods here to the ultimate goal of the paper.
F.1 Homology Groups
This part develops the theory of singular homology to support the claims and analysis in the main text. Other popular homology constructions are discussed in Jacobson [1980]. Informally, the singular homology is built by a succession of mappings between n dimensional blocks and the paths around their boundaries.
F.1.1 Singular Simplex
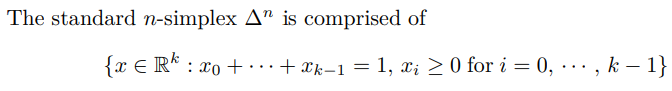
its vertices are the k standard unit vectors and the origin. [112] Familiar examples include:

F.1.2 Singular Chain Complex

F.1.3 Homotopy Invariance

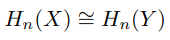
for all n ≥ 0. This means that homology groups are topologically invariants. In particular, if X is a connected contractible space, then all its homology groups are 0 except
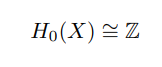
I finish with a sketch of the proof of homotopy invariance of singular homology. A continuous map f : X → Y induces a homomorphism
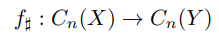
It is easy to see that
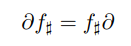
where f♯ is a chain map which descends to homomorphisms on homology
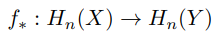
It is left to show that, if f and g are homotopically equivalent, then f∗ = g∗. This implies that if f is a homotopy equivalence then f∗ is an isomorphism. Let F : X × [0, 1] → Y be a homotopy, that takes f to g on the level of chains. It defines a homomorphism
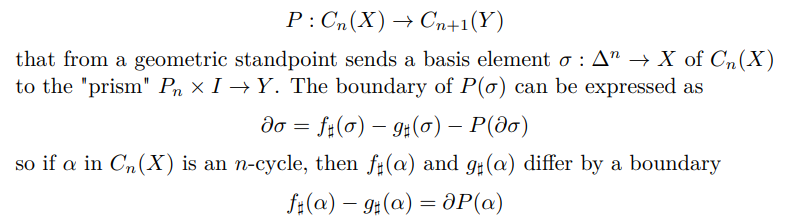
Therefore, they are homologous, which settles the claim.
This paper is available on arxiv under CC 4.0 license.