Author:
(1) David Staines.
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
F.3 De Rham Cohomology
This last mathematical stanza seeks to explain the power of the linear approximation in the most general setting, with a view to justifying major results in the text. This includes the linearization step from (3)-(5) and Decomposition 1, specific to Calvo, and the general bifurcation result Theorem 7. The first subsubsection sets out preliminaries of differential topology and cohomology. The second states the main result. The best textbook here is probably Tu [2011]; some readers may find the informal presentation in Stone and Goldbart [2009] helpful.
F.3.1 Preliminaries

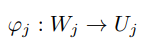
denote the intersection of domains by
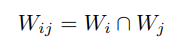
and its map by the two chart maps to the two images
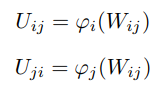
It follows that the transition map between the two charts is the map between the two images of this intersection under the two chart maps.
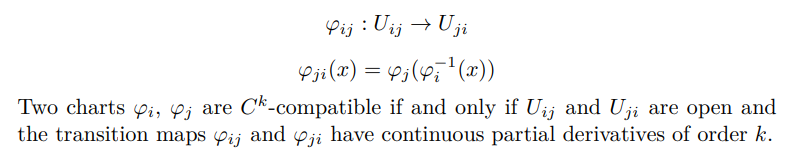
A Differential Form is a coordinate-independent approach to calculus. It has its roots in physics (see Stone and Goldbart [2009]). It differs from the approach to integration in the rest of the paper because it is orientation-dependent, so integrals can be zero or negative for non-zero functions. In general, for a differential form ω integrated over a manifold M and the same manifold but with opposite orientation M′ then
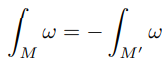
A k form is an object that can be integrated over a k dimensional oriented manifold and is homogeneous of degree k in the coordinate differentials.
A one form can be integrated over an oriented interval [a, b] in the domain of f:
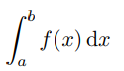
Similarly, the expression
f(x, y, z) dx ∧ dy + g(x, y, z) dz ∧ dx + h(x, y, z) dy ∧ dz
is a 2-form, that has the following integral over an oriented surface S
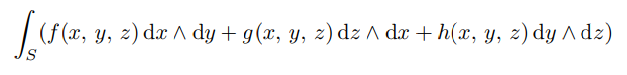
likewise, the 3-form f(x, y, z) dx∧dy∧dz is called a volume element, integrated over an oriented region of three dimensional space. ∧ is called the wedge or Exterior Product. It is an alternating product, in the sense that
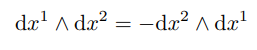

The exterior derivative operator d sends k forms to k+1 forms, so perimeters go to areas, surface areas to enclosed volumes etc. [120] The generalized Stokes theorem states that the integral of a differential form ω over the boundary of some orientable manifold Ω equals the integral of its exterior derivative.
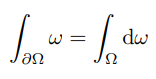
This means that the volume of a sphere is equal to the surface area of the family of spheres covering the circle, as their diameters become arbitrarily small. In general, we can approximate the integral over k + 1- form arbitrarily well, by summing over the boundary of its k form. This constitutes a deep extension of the fundamental theorem of calculus.
Lastly, returning to algebraic topology, it is necessary to introduce Cohomology in general, specifically the Singular Cohomology. Cohomology is the dual construction to homology. It arises from Cochains, which are functions defined on the group of chains in homology theory.
Cohomology develops from the geometry of functions and their pullbacks. Taking two spaces X and Y and a function F on Y , any mapping f : X → Y will lead to another F ◦f called the pullback of F on X under f. Typically, there is interest in the relation between continuity and differentiability properties of the functions. Leading cohomology theories have a product called the Cup Product, which gives them a ring structure. For this reason cohomology can provide richer algebraic invariants.
The singular cohomology is a powerful topological invariant, associating a graded-commutative ring to any topological space.121 Decomposition 1 exemplifies this structure. Every continuous map f : X → Y creates a homomorphism from the cohomology ring of Y to that of X; this puts strong restrictions on the behavior of maps between the two spaces.

Many properties of cohomology are only minor variants of homology:
• Two homotopic maps from X to Y induce the same homomorphism on cohomology (as they do on homology.)
• If a space X is the union of open subsets U and V , then there is a long exact sequence
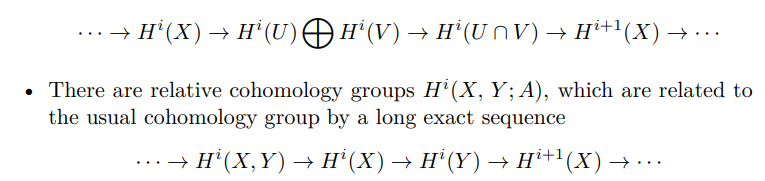
Informally, these properties allow cohomology calculations to be broken down over suitable partitions.

On the other hand, cohomology has a special structure absent in homology. For any topological space X and commutative ring R, there is a bilinear123 map called the Cup Product.
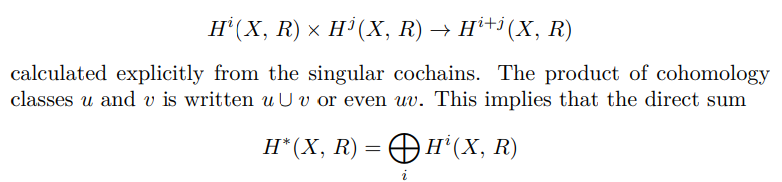


F.3.2 Formalization and Application
The De Rham Cohomology is a technique common to both algebraic and differential topology. It is a powerful tool capable of expressing basic topological information about smooth manifolds, making it easy to compute concrete representations of cohomology classes. It is a cohomology theory based on the behavior of differential forms.
The key distinction is between exact and closed forms. Here, an Exact Form is is a differential form α, that is the exterior derivative of another differential form β, whilst a closed form is a differential form α whose exterior derivative is zero (dα = 0). Thus an exact form is an image of d and a closed form is a kernel of d. Every exact form is closed but a closed form need not be exact. [125] Poincaré’s lemma ensures it is true for contractible spaces. However, there is a critical connection between the existence of exactness and the existence of holes. From this standpoint, the De Rham cohomology measures how the Fundamental Theorem of Calculus [126] fails on general manifolds in higher dimensions.
The De Rham complex is the cochain complex of differential forms on a smooth manifold M with the exterior as its differential:

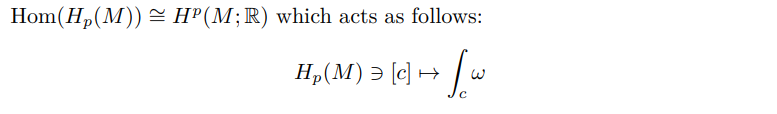
The exterior product endows the direct sum of groups with a ring structure. A further consequence of the theorem is that two cohomology rings are isomorphic, when viewed as graded rings, where the analagous product for the singular cohomology is the cup product.
At last, we come to the application, the cohomology computation for our main model.
Proposition 32. The Calvo Phillips curve model has the following De Rham cohomology representations

In conjunction with Theorem 9, this formally justifies the use of the linear approximations (3)-(5) to represent the non-binding constraint on the representative firm or social planner.
This paper is available on arxiv under CC 4.0 license.