Author:
(1) David Staines.
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
6.3 Literature ComparisonDynamic Stochastic Models
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
6.4 Equilibrium Analysis
This final part sets out local and global properties learned from applying basic analysis techniques and then moves onto discuss their economic and mathematical significance.
Theorem 2. (Surface Estimates / Comparative Statics)
The following relationships exist between stochastic and non-stochastic values

Proofs typically involve applications of Jensen’s and covariance inequalities, along with monotonicity arguments. They are contained in the Appendix A. The next result has a comparative statics flavour but a different style proof. It will be used to specify the distributional consequences of moving from a Non stochastic to a stochastic environment. Beforehand, it is necessary to set out a couple of assumptions defended later on.
Assumption 1. One of the following statements is true: (i) the kernel of the stochastic discount factor M = Eu ′ (Y )/u′ (Y ) covaries positively with profits (ii) all shocks are small (iii) discount factor shocks are small and profits are procyclical (in the sense that Π is stochastically monotone with respect to Y )

Assumption 2. EA is sufficiently large relative to ∆.

The first part follows from the construction of stochastic equilibrium, a suitable comparison of the resetters problem and the distribution of profits at a point in time. The proof of the second part has a microeconomic flavour, involving a suitable Slutsky decomposition. The subsequent remarks clarify the role and significance of the assumptions.
Remark 8. Suppose the economy could accommodate a positive growth rate then we could guarantee that the normalized value of profits with shocks EΠ/A would be below its non-stochastic counterpart. Suppose the economy could accommodate a positive growth rate then we could guarantee that the normalized value of profits with shocks EΠ/A would be below its non-stochastic counterpart.
This idea is fleshed out in Appendix D.2.3. Alternatively we could scale down the units of the labor endowment to make A arbitrarily large.
Remark 9. Assumption 1(i) and (iii) the more appealing alternatives, are not primitive restrictions, thus Proposition 13 is not a true quantitative estimate. Nevertheless, I suspect that a more appealing primitive restriction may arise as a bi-product of rigorous global analysis of the model.
Macroeconomists have traditionally grouped variables into pro and countercyclical, in order to summarize information about the economy. The assumption that gross profits are pro-cyclical is a very weak one. Sales are pro-cyclical (in this model) by definition. Markups would have to be strongly countercyclical to overcome this. In fact recent evidence suggests they are pro-cyclical.[51]Hence, these conditions suffice from an empirical point of view but not from a mathematical vantage, as we have not demonstrated this prediction is consistent with the model. Nevertheless, the approach may be of interest to economic theorists, as it allows one to derive rigorous predictions, without the complexities of in-depth mathematical analysis.[52]
Finally, I am able to confirm that in the patient limit the serious pathology of negative stock prices does not arise.
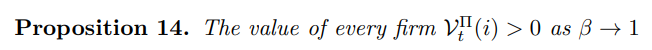
This problem can afflict alternative models with costly price changes. The intuition behind the proof is that as discounting dies away, the value of the firm is dominated by prices in the distant future, by which time the firm will in expectation have had an opportunity to reset its prices and from the point of view of the present, uncertainty will recede as stochastic equilibrium is approached. The result confirms the reconciliation of classical theories of entry and exit with sticky prices- thus supporting neoclassical synthesis and completing this round of comparative analysis.
Therefore, the likely distributional consequences of incorporating uncertainty can be summarized as follows. Relative price distortions will decrease the value of output, which will decrease wages and real marginal costs. In equilibrium, output will fall and labor input will have to increase to make up for some but not all the loss of effective productivity. Profitability will fall. Welfare is lower, indicating that volatility is costly. Finally, uncertainty will cause the interest rate to drop. These findings feel economically intuitive and for the most part should stand up to alternative model details, although the labor supply prediction might change with additional frictions.
Therefore, the likely distributional consequences of incorporating uncertainty can be summarized as follows. Relative price distortions will decrease the value of output, which will decrease wages and real marginal costs. In equilibrium, output will fall and labor input will have to increase to make up for some but not all the loss of effective productivity. Profitability will fall. Welfare is lower, indicating that volatility is costly. Finally, uncertainty will cause the interest rate to drop. These findings feel economically intuitive and for the most part should stand up to alternative model details, although the labor supply prediction might change with additional frictions.
Moreover, the new construction offers further applications.
Corollary 2. When β → 1 the real interest rate r = i − π < 0
Proof. Follows immediately from Theorem 3 (i) and sending β → 1, whilst keeping the shock size fixed.
Very low interest rates were widely documented from the 2008 Global Financial Crisis until the early stages of the COVID pandemic. Long run rates indicate these were expected to continue for a long time.[53] Prominent studies, such as Del Negro et al. [2019], estimated a negative natural rate and estimates fell further during the acute stage of the pandemic (see for example Van der Ghote [2021]). However, non-stochastic growth models cannot support real rates below growth rates.
It is intuitive that in a stochastic environment, government debt without default risk can command a safety (negative risk) premium. Brunnermeier et al. [2020] are able to demonstrate this by deriving a closed form solution to a model, with a financial sector and a bubble in the government debt, solved in continuous time. I am able to dispense with these esoteric assumptions. I therefore show, that this prediction is in fact a general consequence of risk aversion, a fundamental economic mechanism.
In general, the analysis mediates in favor of discrete over continuous time for the majority of macroeconomic applications. Macroeconomists typically adopt continuous time in search of closed form solutions. These require strong functional form assumptions, typically Brownian motion (also called a Wiener process.) Furthermore, unless you have high frequency data, it makes convincing econometrics more challenging. On the other hand, discrete time stochastic equilibrium analysis allows one to obtain quasi-closed forms without specifying particular error distributions, with easily interpretable existence conditions. It also avoids challenges with ascertaining whether derivatives exist, which may not be intuitive in many economic situations.
Finally, stochastic surface solutions provide a promising avenue for parametric comparative statics. Under the limiting assumption justifying the use of standard linearization techniques, we can simply transfer results from the nonstochastic steady state to neighboring stochastic environments. It is instructive to look beyond this case at the effect of larger shocks on comparative statics. I focus on the simplest relationship between price dispersion and the inflation target π.
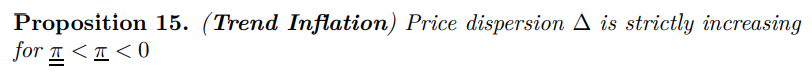
Geometrically the inflation-price dispersion schedule is shifted up and translated to the left in the range of primary interest. Price dispersion will be minimized at a negative rate of trend inflation. This might provide a rationale for deflationary policy.[54] This also has a dynamic interpretation. Stochastic equilibrium pulls down dynamic behavior of price dispersion from a positive trend inflation environment to zero and nearby negative rates of inflation. It suggests there need not be a difference in dynamic behavior between low trend inflation and the low rates of trend deflation typically observed. Hirose [2020] is the only paper I know of to date that looks at trend deflation, in the context of Japan, and he works with a prior trend centered at just −0.214% (see their seventeenth footnote).
Lastly, the analysis here could be of general mathematical and statistical interest. Firstly, the Theorem is an example of mathematical rigidity, in the sense that I have deduced important statistical properties of the solution by analyzing just a single neighborhood. Secondly, the results constitute sharp a priori quantitative estimates of important expectation functionals. They are sharp because the non-stochastic steady state is the limit of the stochastic steady state. They are a priori because we have not yet proven the solution exists; in some instances we will see that a solution does not exist.
In econometric terms, they represent over-identifying conditions. They constitute restrictions on the solution associated with the need for infinite horizon optimization problems to exist. They are the analogy of the steady state that provide additional restrictions on the coefficients of any reduced form representation, like the one presented in the next section. These kind of conditions are rarely seen in statistics where exact identification is predominant or mathematical physics where under-identification is ubiquitous.[55]
Author:
(1) David Staines.
This paper is available on arxiv under CC 4.0 license.
[49] This applies even if we expand our definition of a preference shock to include any disturbance to the financial system. Changes in policy-making have arguably been more significant in many periods- as suggested by studies such as Stock and Watson [2002], Muir [2017] and Ascari et al. [2019].
[50] This means that P(Y (Π1) ≤ y) ≤ P(Y (Π2) ≤ y) if and only if Π1 ≤ Π2.
[51] Nekarda and Ramey [2020] show that the inverse labor share measure directly pertaining to this model is pro-cyclical. Using detailed micro data, Anderson et al. [2023] conclude retail mark ups are weakly pro-cyclical. Domowitz et al. [1986] uncovered similar patterns for manufacturing. Fariñas and Huergo [2003] and Macallan et al. [2008] provide corroborating evidence for a wider set of countries and industries. Nekarda and Ramey [2020] describe how procedures involving more sophisticated production functions can lead to different results that are not relevant in the present setting. Finally, they note how cyclicality would be expected to depend on the distribution of shocks. With Keynesian intuition and their econometric strategy, they suggest that markups were pro-cyclical in response to technology shocks but counter-cyclical when there were shocks to investment.
[52] This strategy should combine profitably with simulations to verify the assumptions.
[53] On July 11th 2020 The Economist reported that Austrian 100 year bonds were yielding just 0.7%. At the ECB’s official target of 2% and assuming a trend growth rate of 2% then it would be reasonable to calculate r − g = −3%.
[54] On this theme, Yun [2005] uses price dispersion to justify temporary deflation in a nonstochastic environment. Schmitt-Grohé and Uribe [2010] discusses alternative rationale for negative inflation. On the other hand, Adam and Weber [2019] are able to rationalize positive inflation by adding heterogeniety in firm level productivity growth into our Calvo framework.
[55] For example, in quantum theory Heisenberg’s uncertainty principle (Heisenberg [1927]) tells us that we cannot know the position and the velocity of an electron, so given the velocity of an electron, its position is unidentified. Conversely, given the speed the position is unidentifiedhence the system as a whole is under-identified. String theorists are interested by mirror symmetry where different shaped universes are observationally equivalent through certain topological lenses (see Greene [2000] and Hartnett [2018]). There are exceptions, for example, researchers studying small sets of rigid bodies that are over-determined. Nevertheless, the concept of over-identification, central to structural econometrics, would seem foreign to the majority of mathematical physicists and the particular kind here are surely novel. This likely explains the failure of mean field game theory to gain traction over DSGE.

