Author:
(1) David Staines.
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
G Further Keynesian Models
The first two subsections lay out two Keynesian models that come up in the course of the discussion in Section 10. The aim is not to solve them out fully but to provide the reader with background. The last part verifies claims made in Section 10.1 concerning unusual policy settings. The idea is that firms reoptimize the price periodically. The difference with Calvo is that they know the length of contract for sure, in advance. Contracts overlap so that in each period the same fraction come up for renewal. This set up seems intuitively appealing.
G.1 Taylor Pricing
The Taylor [1979] model of staggered contracts is one of the most popular in applied macroeconomics. The idea is that firms re-optimize the price periodically. The difference with Calvo is that they know the length of contract for sure, in advance. Contracts overlap so that in each period the same fraction come up for renewal. This set up seems intuitively appealing.
The objective function for a resetting firm is just (24) summed over the length of the contract M. Assume for simplicity at the outset that M = 2, as prominent in the text. The focus is on the small noise limit around ZINSS O( √ ε). For clarity, I will focus on the non-stochastic expansion. It is clear that the price change will be the weighted average of the expected changes in marginal cost and aggregate price level throughout the contract.
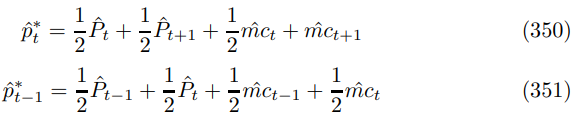
The price level is simply

Lagging this relationship leads to

Hence, (352)-(353)
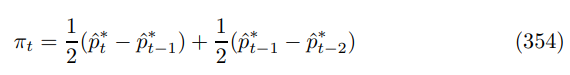
(350)-(351) evaluates to
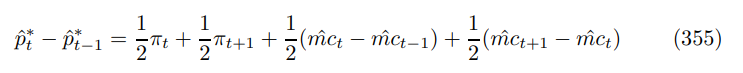
lagging, substituting in, then simplifying yields
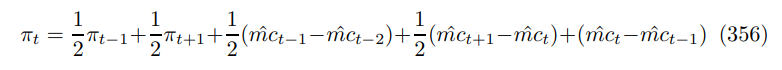
As argued in Section 9.3, inflation is determined half by its lag and half by its lead. Furthermore, the terms occur in difference pairs, so it is clear that the sum of the real coefficients on marginal costs is zero, in keeping with real neutrality. These results extend over to contracts of general length where
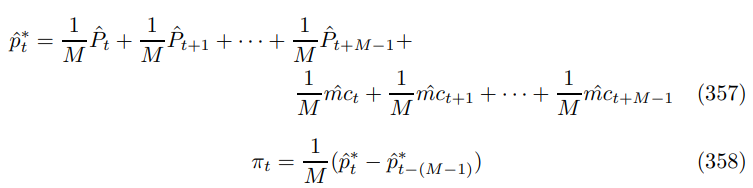
before a similar substitution process yields the Phillips curve
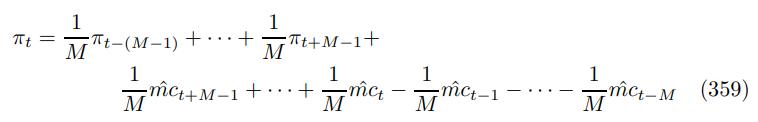
There is a powerful link back to generalized stochastic mean back in Appendix B.2 and crystallized in Proposition 27. The property that the optimal reset price is a weighted average of all the flexible prices extends to inflation determination, if uncertainty and discounting (efficient or otherwise) vanish. This is a universal result.
This paper is available on arxiv under CC 4.0 license.

