Author:
(1) David Staines.
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
5.1 Singular Phillips Curve
This subsection flags up the subtle error in the standard approximation that brings about a purely forward-looking solution. Linearizing the two components of the Phillips curve at ZINSS reveals a special structure, in particular, there is a common root L = 1/αβ in both lag polynomials.
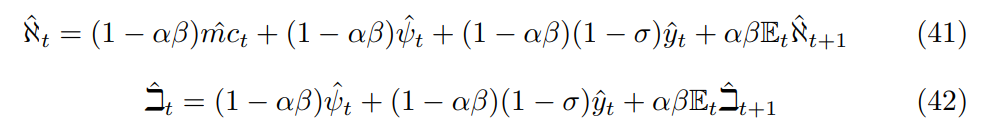
This means the system can be solved by elimination. Therefore, we do not have to lag one of the recursions to perform a substitution introducing lagged terms. The next result confirms that this is unrepresentative of the dynamics of any stochastic system because it only applies when inflation is at steady state where the approximation is irrelevant. Let Lℵ equal the zero of the lag polynomial in ℵ.
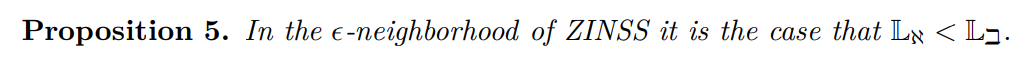
Proof. By elementary manipulation it is clear that this amounts to proving that
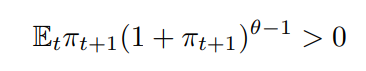
This follows immediately from Chebyshev’s correlation inequality (Lemma 1) which states that
EAB ≥ EA EB
for two strictly increasing functions with equality if and only the measure is degenerate.
ZINSS is an example of a (measure zero) singularity not covered by Proposition 3. In fact it is the wall of the crossing which gives rise to (1). Bifurcation and common roots will be formally connected in Section 9. Thus we arrive at the incorrect step.
Error 1. Cross Equation Cancellation in the Phillips curve
This yields the forward-looking relationship.

where the slope parameter is

to derive an output gap expression first linearize the marginal cost function (38)

Next linearize the production function (36)

now using labor supply constraint and market clearing (19) and (20)
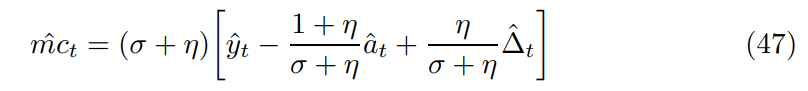
The behaviour of price dispersion is governed by the linearization of (35)
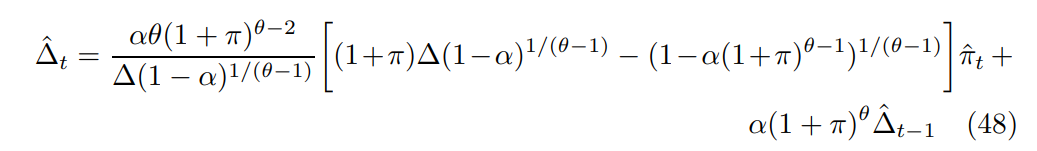
substituting in (π, ∆) = (0, 1) negates the first term leaving

I can use the expression for ZINSS, given in Appendix D, to express the flexible price output in terms of the technology shock as

Substituting into (47) reveals a proportional relationship between changes in marginal costs and the efficient output gap.

Substituting into (43) yields the final form of the Phillips curve

where the form of the composite parameter is
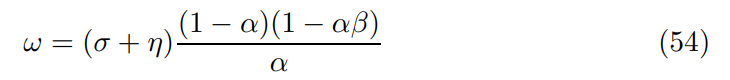
Finally, the approximate Euler equation takes the form
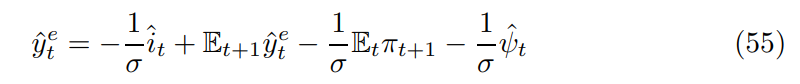
Author:
(1) David Staines.
This paper is available on arxiv under CC 4.0 license.

