Authors:
(1) Edward Crane, School of Mathematics, University of Bristol, BS8 1TH, UK;
(2) Stanislav Volkov, Centre for Mathematical Sciences, Lund University, Box 118 SE-22100, Lund, Sweden.
Table of Links
Reduction to the case of uniform geometry
All original points are eventually removed, a. s.
Acknowledgements and References
6 Coupling Y (⋅) and Z(⋅)
In this section, we complete the proof of Theorem 2. By Lemma 10 it suffices to prove the absolute continuity of the limit point ξ for a B-valued Jante’s law process where B is bounded. So we shall assume throughout this section that B is bounded, and therefore has uniform geometry.
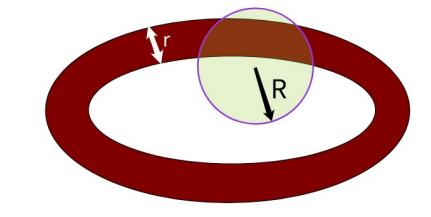
We will need an isoperimetric inequality for inner shells of convex bodies, for which we have been unable to find a reference. It concerns the following problem. Suppose you have a (possibly) hollow chocolate egg whose outer boundary is the boundary of a convex body. If all the chocolate is within distance r of the outer boundary of the egg, what is the maximum quantity of chocolate that can possibly be contained within a ball of radius R? See Figure 4.






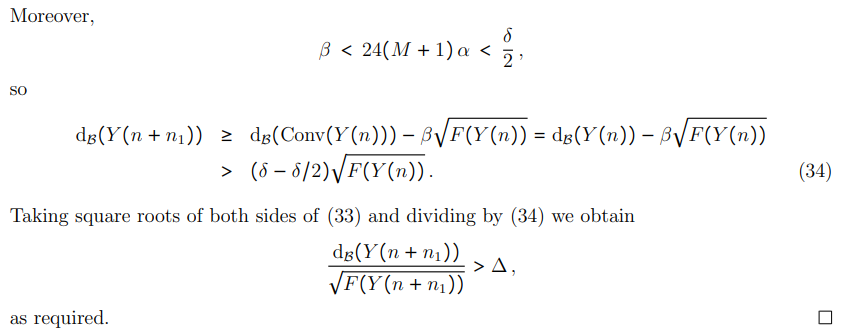


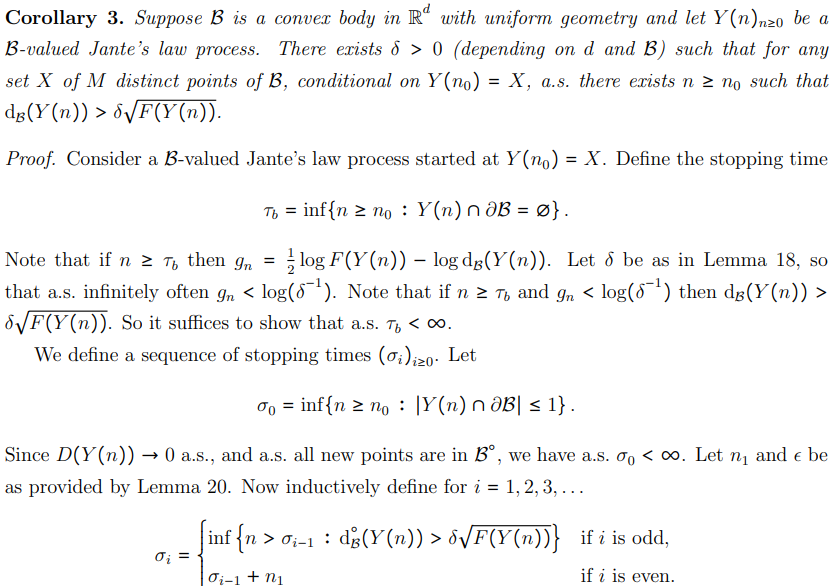
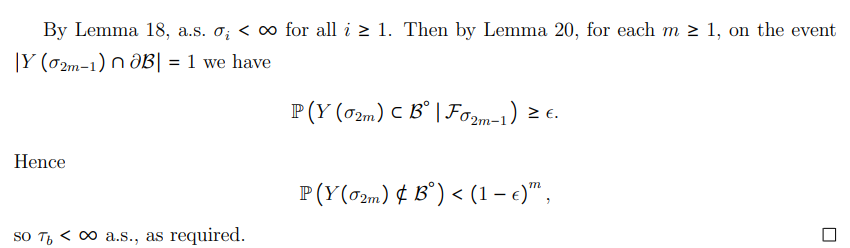


This paper is available on arxiv under CC 4.0 license.
8 Think of δ small and ∆ large.

