Authors:
(1) Edward Crane, School of Mathematics, University of Bristol, BS8 1TH, UK;
(2) Stanislav Volkov, Centre for Mathematical Sciences, Lund University, Box 118 SE-22100, Lund, Sweden.
Table of Links
Reduction to the case of uniform geometry
All original points are eventually removed, a. s.
Acknowledgements and References
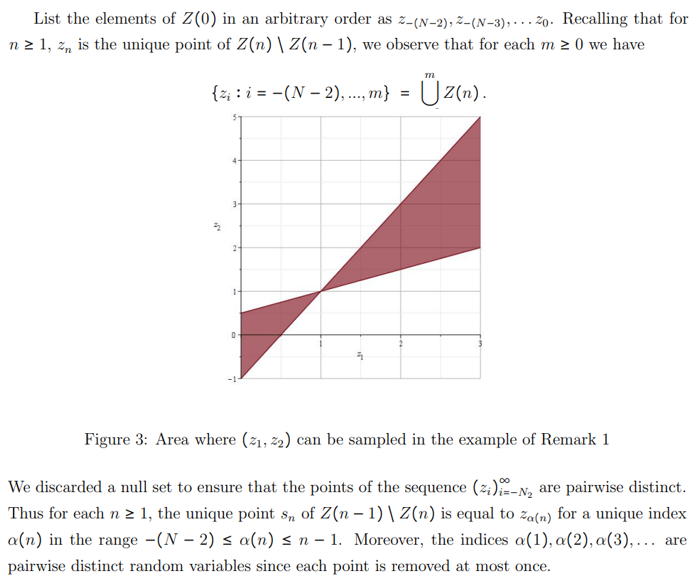
5 Proof of Theorem 1
Without loss of generality, we assume that the initial state Z(0) is deterministic. This is harmless since if for each deterministic choice of Z(0) the limit z∞ exists a.s. and has an absolutely continuous distribution, then if instead Z(0) is random, z∞ still exists a.s. and its distribution is a mixture of absolutely continuous distributions, which is necessarily absolutely continuous.



This paper is available on arxiv under CC 4.0 license.
7 i.e., a set defined by a number of polynomial inequalities and equalities; in our case, a.s. these will be just inequalities.

