Author:
(1) David Staines.
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
9.2 Algebraic Aspects (I) Singularities and Covers
At the end of this subsection, I precisely describe the behavior of the non-linear system local to the ZINSS. Beforehand, I develop the requisite material from algebraic topology.
Definition 8. Let Y be a topological space. A covering space of Y is a topological space X with a surjective (onto) map

Definition 9. A ramification point is where pairs of branches of a covering map meet.

Finally, it helps to have some shorthand notation for all the removable singularities
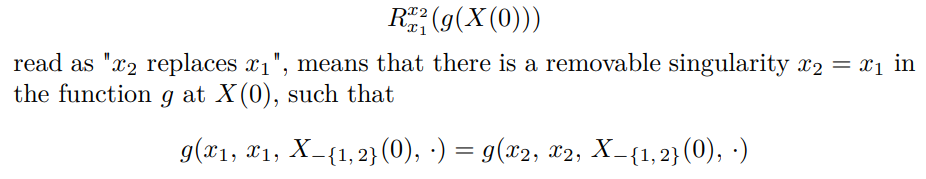
The last ingredient is De Rham’s Theorem (Tu [2011]), which extends differential calculus to manifolds. The idea is that the fundamental theorem of calculus and its immediate implications, hold when appropriately accounting for singular surfaces. All that is required is a differential structure, roughly a formulation of the overall system that is continuously differentiable. It is now possible to reveal the theorem of this subsection.

The construction for the demand shocks is identical, except the cover comes from the non-linear expansion corresponding to (167) and (168) around ZINSS.

The second part justifies the calculations made in 7.2.2. What is happening is that the second order approximations are dropping off, which ensures that the coefficients from past and present shocks will have opposite signs in the first order approximation. The singularities cause them to be conflated and cancel out. This is an exceptional mathematical pathology. This problem is avoided with price dispersion because its covering by inflation is not inter-temporal (there are no lags in its recursion (48)).
This symmetry will prove a universal feature of dynamic responses to shocks affecting efficient resource allocation around the non-stochastic steady state of models with only static market failure, including other Keynesian models. This contrasts with ad hoc shocks to expectations or mark-ups that should not move the efficient allocation and will lack dynamical structure. This symmetry will break down around non-degenerate stochastic equilibrium because there will be differential exposure to uncertainty in other variables. This promises to be a major theme in modern macroeconomics.
Remark 21. The assumption β → 1 is a requirement for the analysis, to ensure there is an inter-temporal covering by a choice variable, as opposed to a shock. When discounting is introduced the covering interpretation breaks down but the singularity will remain and smoothly approach the covering case, as will be demonstrated in the next subsection.
This paper is available on arxiv under CC 4.0 license.
[69] This motivates the cover terminology. The homeomorphic copies in C of an evenly covered neighborhood N form sheets over N. One can think of X as "hovering above" Y, with the horizontal sheets piled up on top of N and the cover C pointing down to the base. Thus the fibers over y consist of those points in X that lie directly above y.